2685. Count the Number of Complete Components
Description
You are given an integer n. There is an undirected graph with n vertices, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting vertices ai and bi.
Return the number of complete connected components of the graph.
A connected component is a subgraph of a graph in which there exists a path between any two vertices, and no vertex of the subgraph shares an edge with a vertex outside of the subgraph.
A connected component is said to be complete if there exists an edge between every pair of its vertices.
Example 1:
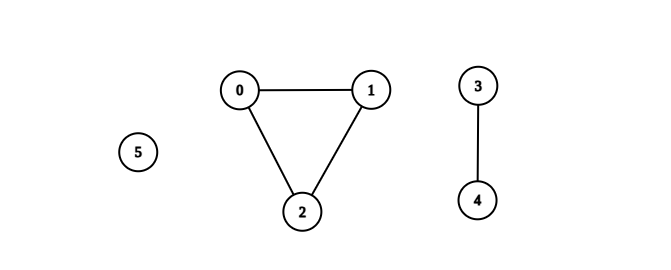
Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4]] Output: 3 Explanation: From the picture above, one can see that all of the components of this graph are complete.
Example 2:
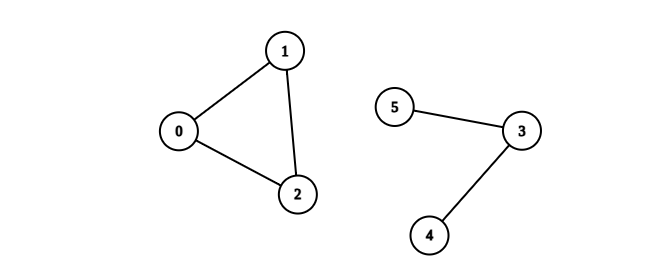
Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]] Output: 1 Explanation: The component containing vertices 0, 1, and 2 is complete since there is an edge between every pair of two vertices. On the other hand, the component containing vertices 3, 4, and 5 is not complete since there is no edge between vertices 4 and 5. Thus, the number of complete components in this graph is 1.
Constraints:
1 <= n <= 500 <= edges.length <= n * (n - 1) / 2edges[i].length == 20 <= ai, bi <= n - 1ai != bi- There are no repeated edges.
Solutions
Solution 1
Python3
class Solution:
def countCompleteComponents(self, n: int, edges: List[List[int]]) -> int:
def dfs(i: int) -> (int, int):
vis[i] = True
x, y = 1, len(g[i])
for j in g[i]:
if not vis[j]:
a, b = dfs(j)
x += a
y += b
return x, y
g = defaultdict(list)
for a, b in edges:
g[a].append(b)
g[b].append(a)
vis = [False] * n
ans = 0
for i in range(n):
if not vis[i]:
a, b = dfs(i)
ans += a * (a - 1) == b
return ans
Java
class Solution {
private List<Integer>[] g;
private boolean[] vis;
public int countCompleteComponents(int n, int[][] edges) {
g = new List[n];
vis = new boolean[n];
Arrays.setAll(g, k -> new ArrayList<>());
for (int[] e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
if (!vis[i]) {
int[] t = dfs(i);
if (t[0] * (t[0] - 1) == t[1]) {
++ans;
}
}
}
return ans;
}
private int[] dfs(int i) {
vis[i] = true;
int x = 1, y = g[i].size();
for (int j : g[i]) {
if (!vis[j]) {
int[] t = dfs(j);
x += t[0];
y += t[1];
}
}
return new int[] {x, y};
}
}
C++
class Solution {
public:
int countCompleteComponents(int n, vector<vector<int>>& edges) {
vector<vector<int>> g(n);
bool vis[n];
memset(vis, false, sizeof(vis));
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
}
function<pair<int, int>(int)> dfs = [&](int i) -> pair<int, int> {
vis[i] = true;
int x = 1, y = g[i].size();
for (int j : g[i]) {
if (!vis[j]) {
auto [a, b] = dfs(j);
x += a;
y += b;
}
}
return make_pair(x, y);
};
int ans = 0;
for (int i = 0; i < n; ++i) {
if (!vis[i]) {
auto [a, b] = dfs(i);
if (a * (a - 1) == b) {
++ans;
}
}
}
return ans;
}
};
Go
func countCompleteComponents(n int, edges [][]int) (ans int) {
g := make([][]int, n)
vis := make([]bool, n)
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
var dfs func(int) (int, int)
dfs = func(i int) (int, int) {
vis[i] = true
x, y := 1, len(g[i])
for _, j := range g[i] {
if !vis[j] {
a, b := dfs(j)
x += a
y += b
}
}
return x, y
}
for i := range vis {
if !vis[i] {
a, b := dfs(i)
if a*(a-1) == b {
ans++
}
}
}
return
}
Solution 2: Simple Method
Problems needed to solve:
How do we maintain the link state between each node and the others? 如
How can one determine whether multiple points form a connected graph?
For the first one: we can maintain each node's connection set(including itself).
For the second one: After solving the first one, we can see:
the node itself includes every node in the connected graph(including itself).
and only connected to the nodes in the connected graph.
Take example 1 to explain:
Node 5's connected node is itself, so it is a connected graph.
Node 0's connected 0, 1, 2. Same as nodes 1, 2.
Nodes 3 and 4 also include themselves and each other.
C++
class Solution {
public:
int countCompleteComponents(int n, vector<vector<int>>& edges) {
int ans = 0;
vector<set<int>> m(n + 1, set<int>());
for (int i = 0; i < n; i++) {
m[i].insert(i);
}
for (auto x : edges) {
m[x[0]].insert(x[1]);
m[x[1]].insert(x[0]);
}
map<set<int>, int> s;
for (int i = 0; i < n; i++) {
s[m[i]]++;
}
for (auto& [x, y] : s) {
if (y == x.size()) {
ans++;
}
}
return ans;
}
};