2268. Minimum Number of Keypresses 🔒

中文文档

Description

You have a keypad with 9 buttons, numbered from 1 to 9, each mapped to lowercase English letters. You can choose which characters each button is matched to as long as:

• All 26 lowercase English letters are mapped to.
• Each character is mapped to by exactly 1 button.
• Each button maps to at most 3 characters.

To type the first character matched to a button, you press the button once. To type the second character, you press the button twice, and so on.

Given a string s, return the minimum number of keypresses needed to type s using your keypad.

Note that the characters mapped to by each button, and the order they are mapped in cannot be changed.

 

Example 1:

Input: s = "apple"
Output: 5
Explanation: One optimal way to setup your keypad is shown above.
Type 'a' by pressing button 1 once.
Type 'p' by pressing button 6 once.
Type 'p' by pressing button 6 once.
Type 'l' by pressing button 5 once.
Type 'e' by pressing button 3 once.
A total of 5 button presses are needed, so return 5.

Example 2:

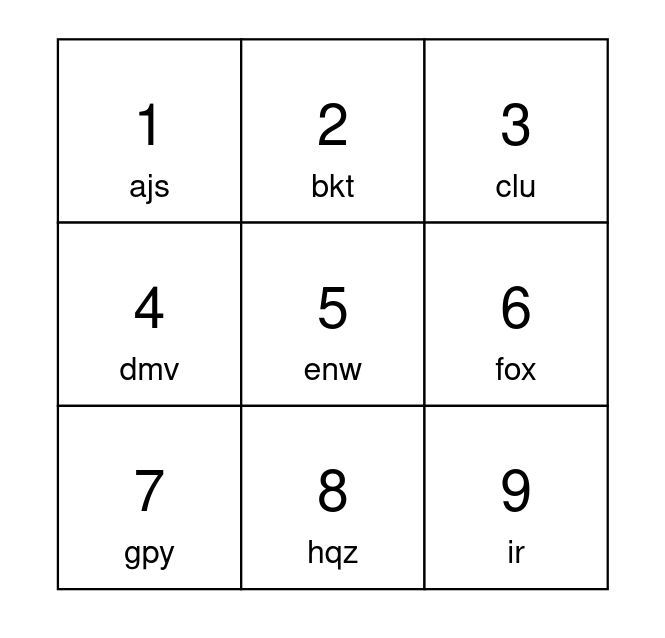
Input: s = "abcdefghijkl"
Output: 15
Explanation: One optimal way to setup your keypad is shown above.
The letters 'a' to 'i' can each be typed by pressing a button once.
Type 'j' by pressing button 1 twice.
Type 'k' by pressing button 2 twice.
Type 'l' by pressing button 3 twice.
A total of 15 button presses are needed, so return 15.

 

Constraints:

• 1 <= s.length <= 105
• s consists of lowercase English letters.

Solutions

Solution 1: Counting + Greedy

First, we count the occurrence of each character in the string $s$, and record it in an array or hash table $\textit{cnt}$.

The problem requires minimizing the number of key presses, so the $9$ most frequent characters should correspond to keys $1$ to $9$, the $10$th to $18$th most frequent characters should correspond to keys $1$ to $9$ again, and so on.

Therefore, we can sort the values in $\textit{cnt}$ in descending order, and then allocate them to the keys in the order from $1$ to $9$, adding $1$ to the number of key presses after allocating every $9$ characters.

The time complexity is $O(n + |\Sigma| \times \log |\Sigma|)$, and the space complexity is $O(|\Sigma|)$. Here, $n$ is the length of the string $s$, and $\Sigma$ is the set of characters appearing in the string $s$. In this problem, $\Sigma$ is the set of lowercase letters, so $|\Sigma| = 26$.

Python3

class Solution:
    def minimumKeypresses(self, s: str) -> int:
        cnt = Counter(s)
        ans, k = 0, 1
        for i, x in enumerate(sorted(cnt.values(), reverse=True), 1):
            ans += k * x
            if i % 9 == 0:
                k += 1
        return ans

Java

class Solution {
    public int minimumKeypresses(String s) {
        int[] cnt = new int[26];
        for (int i = 0; i < s.length(); ++i) {
            ++cnt[s.charAt(i) - 'a'];
        }
        Arrays.sort(cnt);
        int ans = 0, k = 1;
        for (int i = 1; i <= 26; ++i) {
            ans += k * cnt[26 - i];
            if (i % 9 == 0) {
                ++k;
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int minimumKeypresses(string s) {
        int cnt[26]{};
        for (char& c : s) {
            ++cnt[c - 'a'];
        }
        sort(begin(cnt), end(cnt), greater<int>());
        int ans = 0, k = 1;
        for (int i = 1; i <= 26; ++i) {
            ans += k * cnt[i - 1];
            if (i % 9 == 0) {
                ++k;
            }
        }
        return ans;
    }
};

Go

func minimumKeypresses(s string) (ans int) {
	cnt := make([]int, 26)
	for _, c := range s {
		cnt[c-'a']++
	}
	sort.Ints(cnt)
	k := 1
	for i := 1; i <= 26; i++ {
		ans += k * cnt[26-i]
		if i%9 == 0 {
			k++
		}
	}
	return
}

TypeScript

function minimumKeypresses(s: string): number {
    const cnt: number[] = Array(26).fill(0);
    const a = 'a'.charCodeAt(0);
    for (const c of s) {
        ++cnt[c.charCodeAt(0) - a];
    }
    cnt.sort((a, b) => b - a);
    let [ans, k] = [0, 1];
    for (let i = 1; i <= 26; ++i) {
        ans += k * cnt[i - 1];
        if (i % 9 === 0) {
            ++k;
        }
    }
    return ans;
}